Water Loss Kinetics

Written by:

Robert McIntyre

Mazur is a prolific Cryobiologist, and one of his first papers was to describe what happens to cells suspensions as they are cooled and extracellular ice forms.

1963 Mazur – Kinetics of Water Loss from Cells at Subzero Temperaturs and the Likelyhood of Intracelluar Freezing (J. General Physiology)

He creates a differential equation to model the loss of water from a cell as the amount of extracellular ice increases. It's based on balancing the vapor pressures of ice and water in the presence of 1.) Salts which accululate as ice forms and depress freezing point of the remaining water and 2.) The prescence of a cell with a membrane which is modeled as impermeable to salts with a temperature-dependent permeability to water.

He gets a formula with no closed form solution which must be solved numerically, and derives the classic shrinkage curves for various simulated cells with various cooling velocities. Solving these equations was actually a challenge back in 1963:

The equation was solved on an IBM 7090 digital computer by M. T. Harkrider of the Mathematics Division, Oak Ridge National Laboratory, using the Runge-Kutta method for second-order differential equations (Korn and Korn, 1961). I am most indebted to him for this essential part of the study.

Fahy later also developed a simpler, linear differential equation which is easier to solve.

For fun, I decided to model these same equations using matlab and Sussman's scmutils:

;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
;;  Mazur Water Loss  ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;

;; Just a reference temperature
(define T_g 293)
;; cell permeability temp coef. @ T_g
(define b 0.0325)
;; Gas Constant
(define R 8.205736e13) ; (u^2 atm / (mole degree))
;; Molar heat of fusion of ice
(define L_f 5.95e16) 
;; Molar volume of pure water
(define v_1^0 1.8e13) ; (cubic micrometers per mole)
(define V_w v_1^0); fahy's name for it.

(define (C->K celsius) (+ 273.15 celsius))
(define (K->C kelvin) (- kelvin 273.15))

;; freezing temperature of cytoplasm
(define freezing 272)
(define coldest (- freezing 30))

;; (define (make-plot) 
;;   (frame (+ freezing 0.05) coldest -0.01 1))

(define (make-plot) 
  (frame (C->K 0) (C->K -20) -0.01 1))

(define plot (make-plot))

;; molality of cytoplasm in yeast.
(define m 0.5) 

;; use runge-kutta for integration
(set-ode-integration-method! 'qcrk4)

(define (temperature state) (ref state 0))
(define (volume state) (ref state 1))
(define (volume-change state) (ref state 2))

(define ((cell-system-derivative L_f v_1^0 T_g R b
                                 A k_g n_s B) state)
  (let* ((T  (temperature state))
         (V  (volume state))
         (dV (volume-change state))
         (exponential-term (exp (* b (- T_g T))))
         (constant-term (/ (* L_f A k_g) (* B v_1^0)))
         (dV-term
          (- (* exponential-term (+ (* T b) 1))
             (/ (* A R k_g n_s (square T))
                (* B V (+ V (* n_s v_1^0)))))))
    (up 
     1
     dV
     (/ (+ constant-term (* dV dV-term)) 
        (* T exponential-term)))))

(define ((plot-volume-ratio win initial-volume) state)
  (plot-point win (temperature state) 
              (/ (volume state) initial-volume)))

(define (surface-area->volume surface-area)
  (let* ((r    (sqrt (/ surface-area 4 pi)))
         (volume (* (/ 4 3) pi (expt r 3))))
    volume))

(define (radius->surface-area r)
  (* 4 pi (square r)))

(define (initial-water->n_s initial-water)
  ;; takes initial water in cubic micrometers, and converts into 
  ;; osmoles of solute in the cell.
  (* initial-water 
     1e-18 ;; convert cubic micrometers to cubic meters
     1000 ;; liters in a cubic meter, assuming density of water is 1 
     m ;; molality of water in cytoplasm in yeast
     ))


;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
;;  Mazur Water Loss  ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;

(define (plot-mazur-cooling-curve window cell cooling-rate)
  (let ((A    (ref cell 0))
        (k_g  (ref cell 1))
        (n_s  (ref cell 2))
        (initial-volume-of-water (ref cell 3))
        (B    cooling-rate))
    ((evolve 
      cell-system-derivative
      L_f v_1^0 T_g R b
      A k_g n_s B)
     (up freezing                ;Starting Temperature = 0 degrees C
         initial-volume-of-water
         0)                      ;Starts @ equilbrium -- no flow
      (plot-volume-ratio window initial-volume-of-water)
      1e-2                   ;step between plotted points
      coldest                ;final temerature
      1.0e-4                 ;local error tolerance
      )))                    ;initial integration step


(define ((mazur-equilibrium-curve cell) T)
  (let* ((initial-volume-of-water (ref cell 3))
         (n2 (ref cell 2))
         (t (exp (* L_f (/ R) (- (/ 273) (/ T)))))
         (u (* v_1^0 n2)))
    (/ (/ (* t u) (- 1 t)) initial-volume-of-water)))
  
(define (plot-mazur-equilibrium-curve window cell)
  (let ((equilb-curve (mazur-equilibrium-curve cell)))
    (begin
      (plot-point window freezing 1.)
      (map 
       (lambda (T) (plot-point window T (equilb-curve T)))
       (iota 2000 freezing (/ (- coldest freezing) 2000.)))
      (plot-line window 
                 freezing 1. 
                 freezing (equilb-curve freezing))
      1)))

(define mazur-yeast-cell
  (let* ((diameter 5.84)
         (radius (/ diameter 2))
         (initial-water 88))
  (list
   (radius->surface-area radius)  ; A
   0.3                            ; k_g
   (initial-water->n_s initial-water)
   initial-water                  ; initial volume of water, 
   )))                            ; cubic micrometers

(define (plot-mazur-figure-2-a)
  (let ((plot (make-plot)))
    (plot-mazur-equilibrium-curve plot mazur-yeast-cell)
    (plot-mazur-cooling-curve plot mazur-yeast-cell -1)
    (plot-mazur-cooling-curve plot mazur-yeast-cell -10)
    (plot-mazur-cooling-curve plot mazur-yeast-cell -100)
    (plot-mazur-cooling-curve plot mazur-yeast-cell -1000)
    (plot-mazur-cooling-curve plot mazur-yeast-cell -10000)))

(define mazur-rbc
  (list
   163          ; A   -- area (square micrometers)
   5.           ; k_g -- Permeability constant 
   1.83e-14     ; n_s -- osmoles of solute in cell
   61))         ; initial water

(define (plot-mazur-rbc)
  (let ((plot (make-plot)))
    (plot-mazur-equilibrium-curve plot rbc)
    (plot-mazur-cooling-curve plot rbc (* -1000 1))
    (plot-mazur-cooling-curve plot rbc (* -1000 2.5))
    (plot-mazur-cooling-curve plot rbc (* -1000 5))
    (plot-mazur-cooling-curve plot rbc (* -1000 7.5))
    (plot-mazur-cooling-curve plot rbc (* -1000 10))))

;; finally did it!


;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
;;;;  Fahy Water Loss  ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;

(define ((cell-system-derivative-fahy
          L_f V_w T_g R b A k_g n_s B I S) state)
  (let* ((T (temperature state))
         (T_c  (- T 273.15))
         (V  (volume state))
         
         (water-activity-polynominal
          (+ 1 (* 0.00966 T_c) (* 4.1025e-5 (square T_c))))
          
         (cell-solute-mole-fraction
          (/ (+ 1 (/ V (* n_s V_w)))))

         (log-term
          (/ (- 1 (* I cell-solute-mole-fraction)
                (* S (square cell-solute-mole-fraction)))
              water-activity-polynominal))

         (factored-term
          (* (- k_g) (exp (* b (- T T_g))) A R T (/ B) (/ V_w))))
    (up 
     1
     (* factored-term (log log-term)))))

(define (plot-fahy-cooling-curve 
         window cell soln cooling-rate initial-temperature)
  (let ((A    (ref cell 0))
        (k_g  (ref cell 1))
        (n_s  (ref cell 2))
        (initial-volume-of-water (ref cell 3))
        
        (I (ref soln 0))
        (S (ref soln 1))
        
        (B    cooling-rate))

    ((evolve 
      cell-system-derivative-fahy
      L_f V_w T_g R b A k_g n_s B I S)
     (up initial-temperature ;; need to manually adjust to match reality
         initial-volume-of-water) 
      (plot-volume-ratio window initial-volume-of-water)
      1e-2                   ;step between plotted points
      (C->K -20)                ;final temerature
      1.0e-8                 ;local error tolerance
      )))                    ;initial integration step

(define (dpass a)
  (display a) (newline) a)

(define ((fahy-equilibrium-curve cell soln) T)
  (let* ((initial-water (ref cell 3))
         (T_c (- T 273.15))
         (X* (+ (* -0.00966 T_c) (* -4.1025e-5 (square T_c))))
         (I (ref soln 0))
         (S (ref soln 1))
         (n_s (ref cell 2)))
    (* 
     (/ initial-water)
     (if (= S 0)
         ;; Ideal Solute
         (* V_w n_s (- (/ X*) 1))
         ;; Non Ideal Solute
         (* V_w n_s 
            (- (/ (* 2 S) 
                  (- (sqrt (+ (square I) (* 4 S X*))) I)) 1))))))

(define (plot-fahy-equilibrium-curve window cell soln)
  (let ((equilb-curve (fahy-equilibrium-curve cell soln)))
    (begin
      (map 
       (lambda (T) (plot-point window T (equilb-curve T)))
       (iota 2000 (C->K -0.93) (/ (- (C->K -20) (C->K -0.93)) 2000.)))
      1)))

(define water
  (list 
   1 ;; I 
   0 ;; S
   ))

(define DMSO-ideal water)

(define DMSO-non-ideal
  (list
   0.9107 ;; I 
   4.1667 ;; S
   ))

(define fahy-DMSO-cell
  (list 
   107 ;; A
   0.3 ;; k_g
   13.2e-14 ;; n2
   81.75 ;; initial water
   ))

(define (plot-fahy-figure-1-DMSO plot)
  (plot-fahy-equilibrium-curve plot fahy-DMSO-cell DMSO-non-ideal)
  (plot-fahy-equilibrium-curve plot fahy-DMSO-cell DMSO-ideal)
  (plot-fahy-cooling-curve 
   plot fahy-DMSO-cell DMSO-ideal      -100 (C->K -2.8))
  (plot-fahy-cooling-curve 
   plot fahy-DMSO-cell DMSO-non-ideal  -100 (C->K -2.8))
  ))

(define (plot-fahy-figure-1-water plot)
  (plot-fahy-equilibrium-curve plot mazur-yeast-cell water)
  (plot-fahy-cooling-curve 
   plot mazur-yeast-cell water  -10  (C->K -0.93))
  (plot-fahy-cooling-curve 
   plot mazur-yeast-cell water  -100 (C->K -0.93)))

(define (plot-fahy-figure-1)
  (let ((plot (make-plot)))
    (plot-fahy-figure-1-water plot)
    (plot-fahy-figure-1-DMSO plot)))


;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
;;  Comparison / Graphing  ;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;

(define (plot-file name)
  (open-output-file
   (string "/home/r/priv/21cm/water-loss-kinetics/" name)))

;; Redefine plot-point to send it to a file instead of the screen
;; (define (plot-point file x y)
;;   (write-string (string (* 1.0 x)) file)
;;   (write-string "\t" file)
;;   (write-string (string (* 1.0 y)) file)
;;   (newline file)
;;   (flush-output file))

;; (define (plot-line a b c d e) 0)

(define (plot-fahy-figure-1-full)
  ;; DMSO
  (plot-fahy-equilibrium-curve 
   (plot-file "fahy1/dmso-1.dat") fahy-DMSO-cell DMSO-non-ideal)
  (plot-fahy-equilibrium-curve 
   (plot-file "fahy1/dmso-2.dat") fahy-DMSO-cell DMSO-ideal)
  (plot-fahy-cooling-curve 
   (plot-file "fahy1/dmso-3.dat") 
   fahy-DMSO-cell DMSO-ideal -100 (C->K -2.8))
  (plot-fahy-cooling-curve 
   (plot-file "fahy1/dmso-4.dat") 
   fahy-DMSO-cell DMSO-non-ideal  -100 (C->K -2.8))
  
  ;; Yeast in Water -- Fahy
  (plot-fahy-equilibrium-curve 
   (plot-file "fahy1/fahy-water1.dat") mazur-yeast-cell water)
  (plot-fahy-cooling-curve 
   (plot-file "fahy1/fahy-water2.dat") 
   mazur-yeast-cell water -10  freezing)
  (plot-fahy-cooling-curve 
   (plot-file "fahy1/fahy-water3.dat") 
   mazur-yeast-cell water  -100 freezing)

  ;; Yeast in Water -- Mazyr
  (plot-mazur-equilibrium-curve 
   (plot-file "fahy1/mazur-water1.dat") mazur-yeast-cell)
  (plot-mazur-cooling-curve 
   (plot-file "fahy1/mazur-water2.dat") mazur-yeast-cell -10)
  (plot-mazur-cooling-curve 
   (plot-file "fahy1/mazur-water3.dat") mazur-yeast-cell -100))

(define (plot-fahy-mazur)
  (let ((plot (make-plot)))
    (plot-mazur-equilibrium-curve 
     (plot-file "res/mazur-1.dat") mazur-yeast-cell)
    (plot-fahy-equilibrium-curve 
     (plot-file "res/fahy-1.dat") mazur-yeast-cell water)

    (plot-mazur-cooling-curve 
     (plot-file "res/mazur-2.dat") mazur-yeast-cell -1)
    (plot-fahy-cooling-curve 
     (plot-file "res/fahy-2.dat") mazur-yeast-cell water -1 freezing)

    (plot-mazur-cooling-curve 
     (plot-file "res/mazur-3.dat") mazur-yeast-cell -10)
    (plot-fahy-cooling-curve 
     (plot-file "res/fahy-3.dat") mazur-yeast-cell water -10 freezing)

    (plot-mazur-cooling-curve 
     (plot-file "res/mazur-4.dat") mazur-yeast-cell -100)
    (plot-fahy-cooling-curve 
     (plot-file "res/fahy-4.dat") mazur-yeast-cell water -100 freezing)

    (plot-mazur-cooling-curve 
     (plot-file "res/mazur-5.dat") mazur-yeast-cell -1e3)
    (plot-fahy-cooling-curve 
     (plot-file "res/fahy-5.dat") mazur-yeast-cell water -1e3 freezing)
    
    (plot-mazur-cooling-curve 
     (plot-file "res/mazur-6.dat") mazur-yeast-cell -1e4)
    (plot-fahy-cooling-curve 
     (plot-file "res/fahy-6.dat") mazur-yeast-cell water -1e4 freezing)
))

;; testing 
;; (define A (ref mazur-yeast-cell 0))
;; (define k_g  (ref mazur-yeast-cell 1))
;; (define      n_s  (ref mazur-yeast-cell 2))
;; (define I 1)
;; (define S 0)
;; (define B -100)

;; (define T 272)
;; (define T_c  (- T 273.15))
;; (define V 88)
;; (define start (up T V))

I also did this in octave, because why not?

pkg load odepkg

global freezing = 272
global coldest = freezing - 30
global T_g = 293
global R = 82.057e12
global b = 0.0325
global L_f = 5.95e16
global v_w = 1.8e13
global mazur_A = 107.14590240627203
global mazur_k_g = 0.3
global mazur_n2 = 52.14433917105239
global mazur_initial_water = 88

initial_mazur_state = [88, 0]

## Cooling rate
global B = -100

function D = cell_system_derivative(state, T)
  V = state(1)
  dV = state(2)
  global freezing           
  global coldest            
  global T_g                
  global R                  
  global b                  
  global L_f                
  global v_w                
  global mazur_A            
  global mazur_k_g          
  global mazur_n2           
  global mazur_initial_water
  global B

  exponent = exp(b*(T_g - T))
  denominator = T*exponent
  constant = (L_f * mazur_A * mazur_k_g) / (B * v_w)
  dV_term = (b*T + 1) * exponent - (mazur_A * R * mazur_k_g * mazur_n2 * T^2)/(B*V*(V+mazur_n2*v_w))
  d2V = (constant + (dV * dV_term)) / denominator
  D = [dV d2V]
end

Temperature_Range = linspace(freezing, coldest, 9000)

result = lsode(@cell_system_derivative, initial_mazur_state, Temperature_Range)

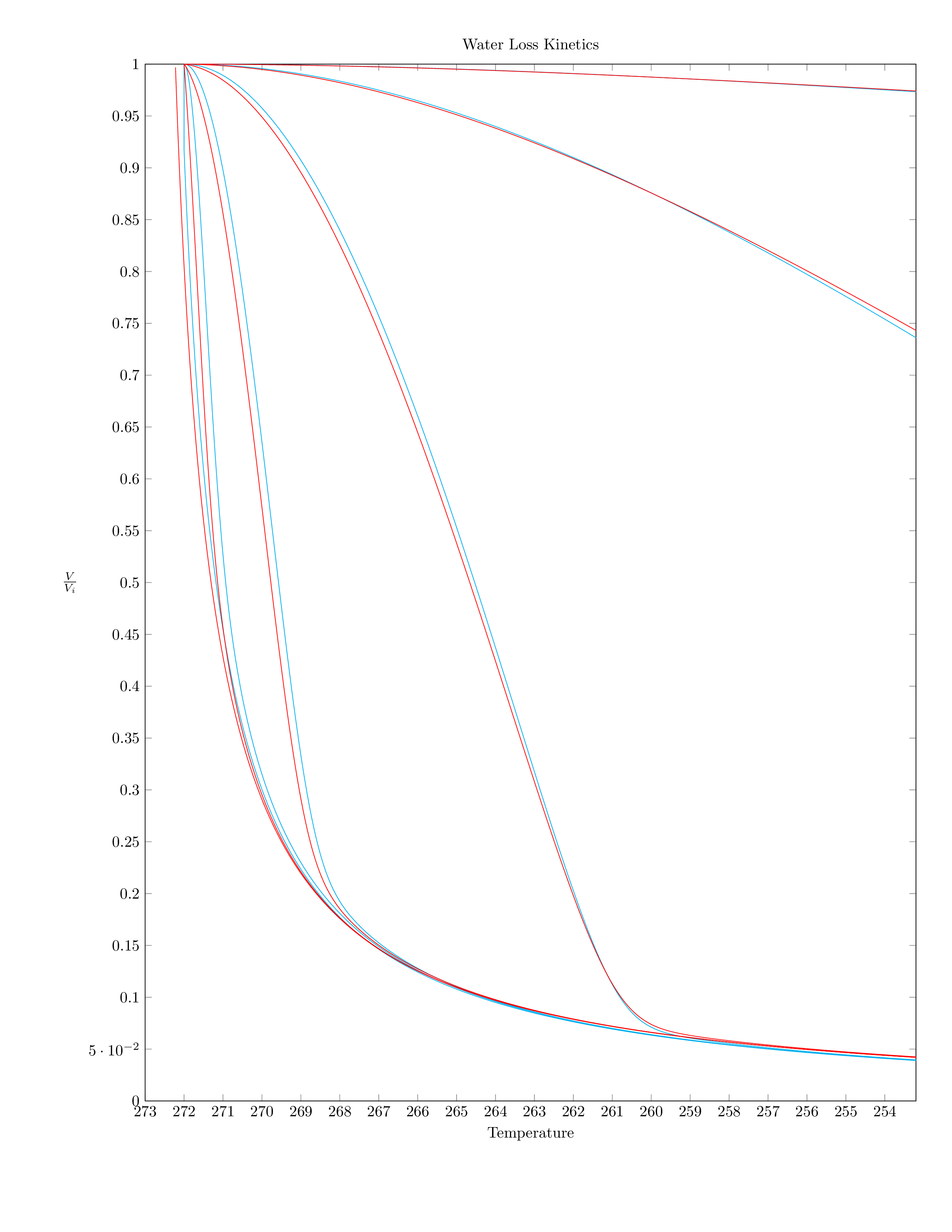
Figure 1: Comparison of Mazur's equation and Fahy's simplified linear differential equation. The two equations give similar results for simulated red blood cells

Water Loss Kinetics

aurellem ☉